高斯过程(Gaussian process),简单的说,就是一系列关于连续域(时间或空间)的随机变量的联合,而且针对每一个时间或是空间点上的随机变量都是服从高斯分布的。
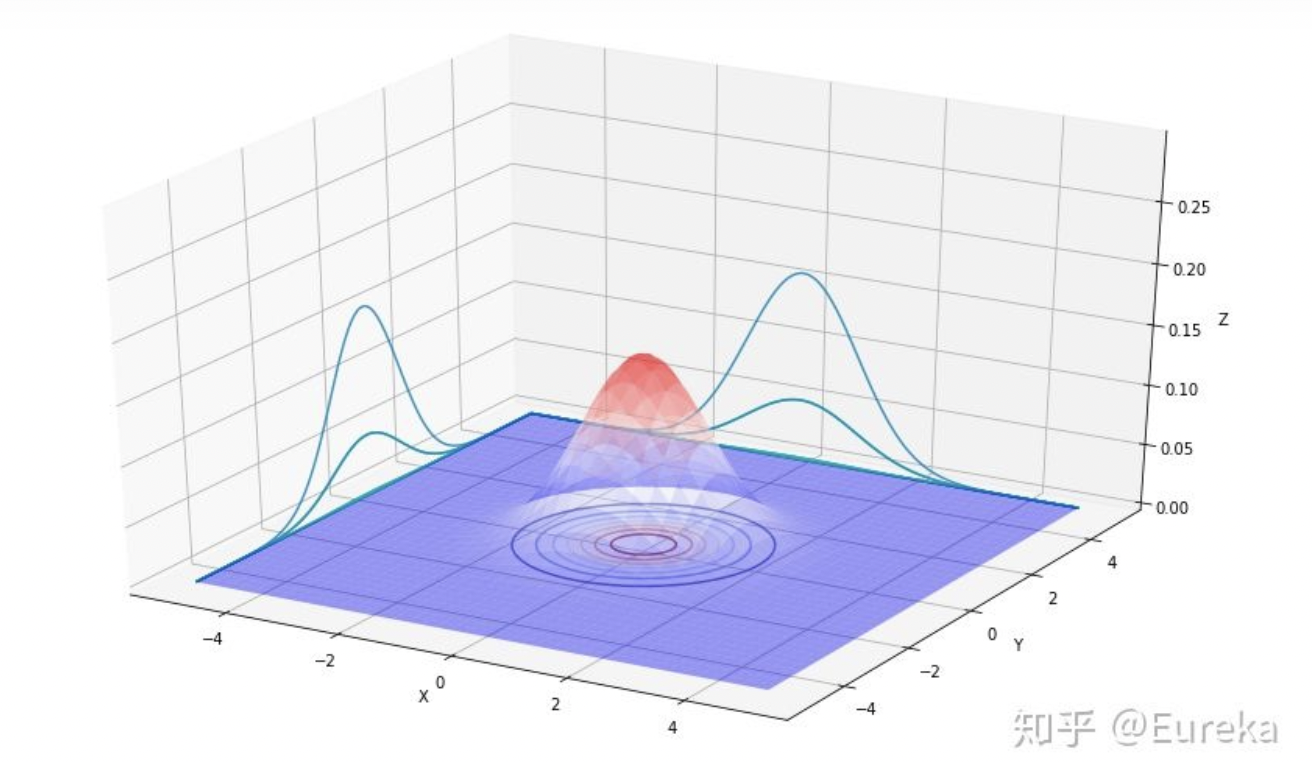
下图就是一个大概的高斯过程的步骤:
- 首先先设定均值,然后随机生成一些先验的函数。
- 根据观测数据得到后验函数。
- 若干这些函数的曲线共同构成了高斯过程给出的置信区间。
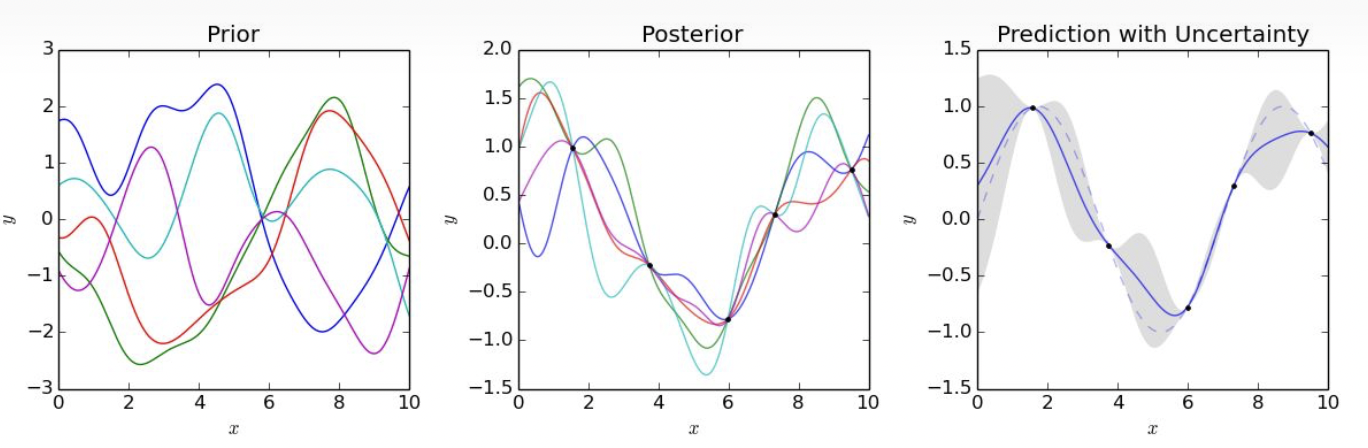
上图一共有5条不同颜色的线,每一条曲线代表了一个GP的样本。首先来看其中的蓝色的线,对应x轴上找一个点,比如x=2大概对应的的y轴约为0.6左右。它所代表的是对应x=2时的一个随机变量$X(x=2)$”正好”出现的点罢了,本质上对应x=2的是一个随机变量而不是一个确定的点。另外对应于任一时刻的随机变量还需要服从一个确定的高斯分布(并不是说所有时刻对应的随机变量需要服从同一个高斯,只是服从的高斯分布的具体参数只跟时刻有关)。除此之外,若是GP的样本,还需要满足的是,任意个点(对应不同时刻的随机变量)联合需要服从多元高斯分布。因此GP的分布就是对于时间域上所有随机变量的联合分布。
既然是满足多元高斯分布,那么必定需要一个确定的mean和确定的covariance 吧。反过来说,若是给定一个mean和covariance,那么自然不同时刻的随机变量的出现的整体位置和相关情况也就被限定住。因此,一个GP可以被mean和covariance function共同唯一决定。
至于covariance function么,这个才是之后在machine learning的应用中被广为探讨的部分,因而就被称为了核函数kernel,原因就是它捕捉了不同输入点之间的关系,并且反映在了之后样本的位置上。这样的话,就可以做到,利用点与点之间关系,以从输入的训练数据预测未知点的值。
高斯过程是一种无参数方法,只通过训练得到,不用关心也不用显式的指定模型长什么样子。
自然底数
$e=(1+1/n)^n\approx2.71828…$
协方差矩阵
$\sum=Cov(X_i,X_j)=E[(X_i-\mu_i)(X_j-\mu_j)^T]$
可以一定程度反映两组分布的线性相关关系
若两组分布独立,那他们的协方差矩阵在非对角线位置都应该是0
一元高斯分布
$f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
$\mu:期望$
$\sigma:方差$
$\frac{1}{\sigma\sqrt{2\pi}}$:个常数项,为了让高斯分布的积分等于1不了/。,
多元高斯分布
无限元高斯分布
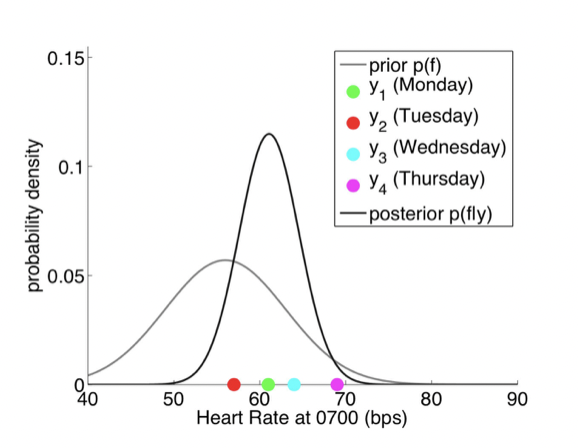
在多元高斯分布的基础上考虑进一步扩展,假设有无限多维呢?用一个例子来展示这个扩展的过程。假设我们在周一到周四每天的 7:00 测试了 4 次心率,如下图中 4 个点,可能的高斯分布如图所示(高瘦的那条)。这是一个一元高斯分布,只有每天 7: 00 的心率这个维度。
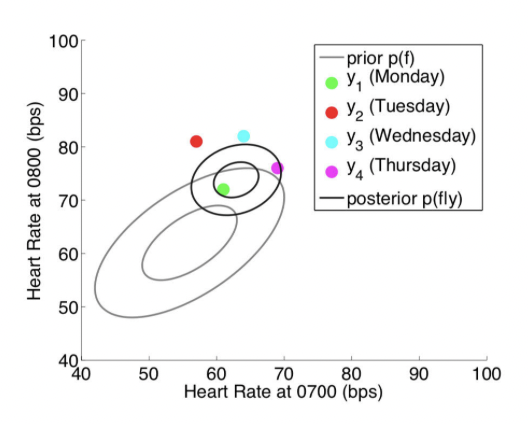
现在考虑不仅在每天的 7: 00 测心率(横轴),在 8:00 时也进行测量(纵轴),这个时候变成两个维度(二元高斯分布)。
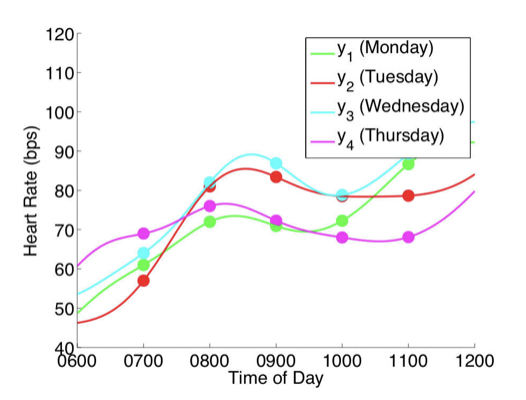
更进一步,如果我们在每天的无数个时间点都进行测量,则变成了下图的情况。注意下图中把测量时间作为横轴,则每个颜色的一条线代表一个(无限个时间点的测量)无限维的采样。当对每次对无限维进行采样得到无限多个点时,其实可以理解为我们采样得到了一个函数。
当从函数的视角去看待采样,理解了每次采样无限维相当于采样一个函数之后,原本的概率密度函数不再是点的分布 ,而变成了函数的分布。这个无限元高斯分布即称为高斯过程。高斯过程正式地定义为:对于所有 $x=[x_1,x_2,⋯,x_n] ,f(x)=[f(x_1),f(x_2),⋯,f(x_n)] $都服从多元高斯分布,则称 f 是一个高斯过程,表示如下:
$f(x)\sim N(\mu(x),k(x,x))$
这里 $μ(x):\mathbb{R}^n→\mathbb{R}^n$表示均值函数(Mean function),返回各个维度的均值;$k(x,x):\mathbb{R}^n×\mathbb{R}^n→\mathbb{R}^n$ 为协方差函数 Covariance Function(也叫核函数 Kernel Function)返回两个向量各个维度之间的协方差矩阵。一个高斯过程为一个均值函数和协方差函数唯一地定义,并且一个高斯过程的有限维度的子集都服从一个多元高斯分布(为了方便理解,可以想象二元高斯分布两个维度各自都服从一个高斯分布)。
参考
什么是Gaussian process? —— 说说高斯过程与高斯分布的关系