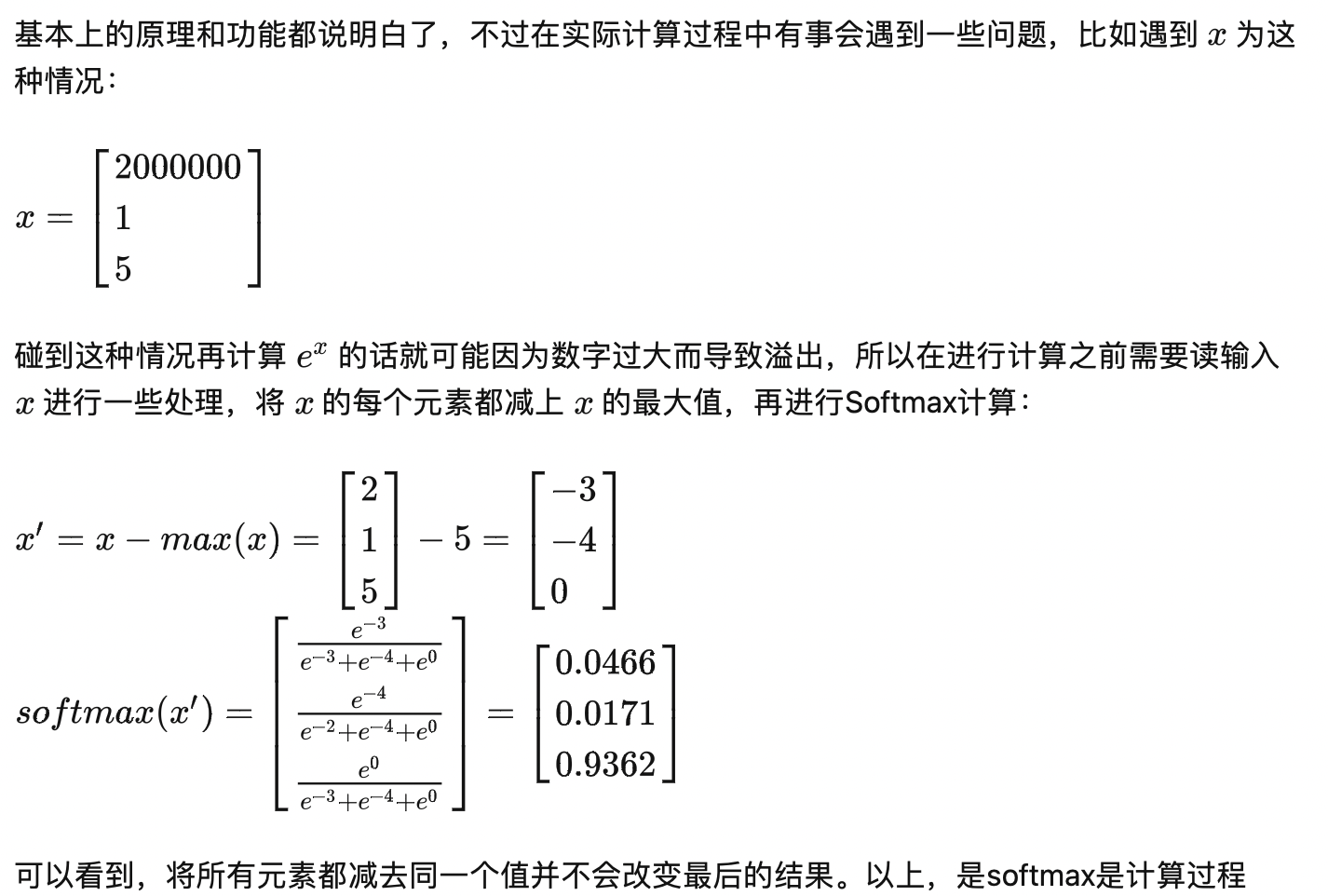
首先介绍一下Softmax的公式:
$a_i=\frac{e^{z_i}}{\sum_j^ne^{z_j}}$
它接受一个向量(或者一组变量)作为输入,每个变量指数化后除以所有指数化变量之和,有点类似于对输入进行归一化,事实上它就叫做归一化指数函数。
Sigmoid函数其实就是Softmax在二分类时候的特例,对于二分类而言(以输入$x_1$ 为例):
Sigmoid函数: $output(x_1)=\frac{1}{1+e^{-x_1}}$ (1)
Softmax函数: $output(x_1)=\frac{e^{x_1}}{e^{x_1}+e^{x_2}}=\frac{1}{1+e^{-(x_1-x_2)}}$ (2)
由公式(2)我们可知,$(x1−x2)$ 可以用$z_1$代替,即Softmax函数可以写成:
$output(z_1)=\frac{1}{1+e^{-z_1}}$ (3)
(3)和公式(1)完全相同,所以理论上来说两者是没有任何区别的。