幂运算(英语:exponentiation),又称指数运算,是数学运算,表达式为$b^n$,读作“b的n次方”或“b的n次幂”。其中, b称为底数,而n称为指数,通常指数写成上标,放在底数的右边。如果指数很大,通常幂运算的结果都特别大,而且很慢,那么有没有一种好的方法可以加速这一计算过程呢。
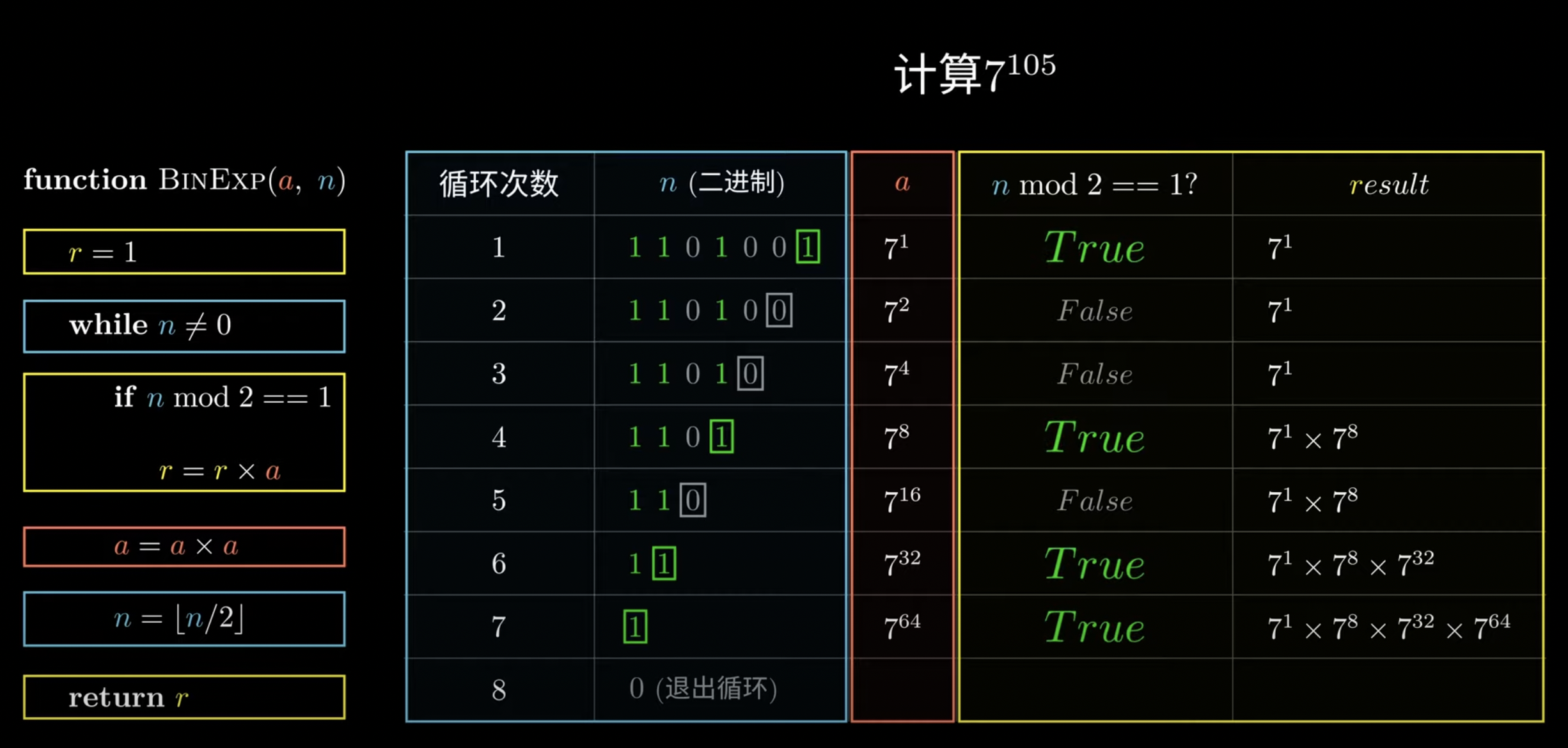
def fast_exp(a, n):
"""
快速求幂函数的结果,时间复杂度为O(logn)
:param a: 底数
:param n: 指数
:return: 运算结果
"""
r = 1
while n != 0:
if n & 1 == 1: #其操作等价于对2取模
r = a * r
a *= a
n = n >> 1 #其操作等价于n除以2并向下取整
return r快速幂算法的应用有以下三点:
计算$a^n$对$m$取模
幂取模运算在密码学和数论中非常重要。


计算斐波那契数列第n项
求斐波那契数列第n项只需要将初始化的r改为矩阵形式即可。

def fast_fab(n):
A = np.array([1, 0])
R = np.array([[1, 1], [1, 0]])
I = np.eye(2)
while n != 0:
if n & 1 == 1:
I = I @ R
R = R @ R
n = n >> 1
return I @ A线性变换n次
类似于斐波那契数列算法




